A statistic is a descriptive measure of a sample. Statistics are usually denoted by Roman letters. Examples of statistics are:

 

	sample mean	xbar
s2	sample variance
s	sample standard deviation

 

A statistic is a measure on the items in a random sample. Since the only reason to ever draw a random sample is to infer something about the population from which it came, it should be clear that when we calculate a given statistic we only do so in order to estimate a corresponding parameter of the population from which the sample was drawn. An example of a statistic is the mean (i.e. average) of the measures in the sample.

 

As indicated by the central limit theorem, the mean of a random sample can be used to estimate the mean of the population from which the sample was taken.[1]

 

 

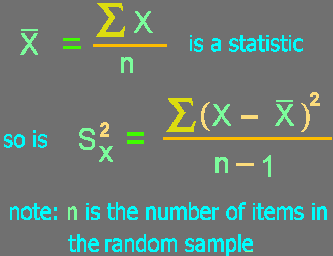
Differentiation between the terms parameter and statistic is important only in the use of inferential statistics. This is because the calculation of parameters is usually either impossible or infeasible because of the amount of time and money required to gather data about the whole population under study. In such case, the researcher can take a random sample of the population, calculate a statistic on the sample, and infer by estimation the value of the parameter.

 

Unless parameters are computed directly from the population, the statistician never knows with certainty whether the estimates or inferences made from samples are true.

 

Inferences about parameters are made under uncertainty.

 

The basis for inferential statistics then is the ability to make decisions about parameters without having to complete a census of the population.